#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10; 
/*
01背包：
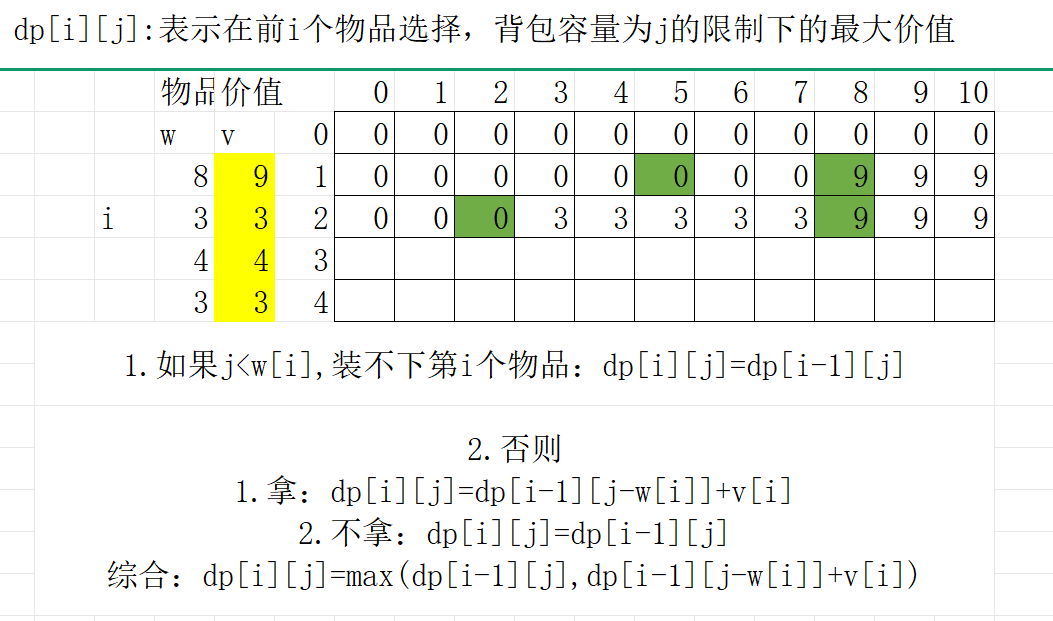
状态表示：dp[i][j]:表示在前i个物品选择，背包容量为j的限制下的最大价值
状态转移方程：
	1.如果j<w[i],装不下第i个物品：dp[i][j]=dp[i-1][j]
	2.否则
		1.拿：dp[i][j]=dp[i-1][j-w[i]]+v[i]
		2.不拿：dp[i][j]=dp[i-1][j]
	综合：dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]) 
*/
int n,w;//n物品数量  w是背包容量 
int c[N],v[N];//V数组是花费    C数组是价值
int dp[N][N];//表示在前i个物品选择，背包容量为j的限制下的最大价值
int main(){
	cin>>n>>w;
	for(int i=1;i<=n;i++) cin>>c[i];
	for(int i=1;i<=n;i++) cin>>v[i];
	for(int i=1;i<=n;i++){
		for(int j=0;j<=w;j++){
			if(j<v[i]) dp[i][j]=dp[i-1][j];
			else dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+c[i]); 
		}
	}
	cout<<dp[n][w];
    return 0;
}