从2024.8.25号开始，就要离开老赛码了，呜呜呜呜呜呜呜呜呜呜

冲刺777道（要走了冲刺不了了呜呜呜呜呜呜呜呜呜）

ybhome.iok.la:8888 集训域

/*
       ┏┓　　　┏┓
     ┏┛┻━━━┛┻┓
     ┃　　　　　　　┃
     ┃　　　━　　　┃
     ┃　┳┛　┗┳　┃
     ┃　　　　　　　┃
     ┃　　　┻　　　┃
     ┃　　　　　　　┃
     ┗━┓　　　┏━┛Codes are far away from bugs with the animal protecting
         ┃　　　┃    神兽保佑,代码无bug
         ┃　　　┃
         ┃　　　┗━━━┓
         ┃　　　　　 ┣┓
         ┃　　　　 ┏┛
         ┗┓┓┏━┳┓┏┛            orz orz orz orz orz
           ┃┫┫　┃┫┫			   orz orz orz orz orz
           ┗┻┛　┗┻┛     ○|￣|_  orz orz orz orz orz
*/

图（关系结构）

由点和边构成的集合

• 无向图
• 有向图

带权图

度

出度：从一个点出去的边的数量

入度：进入一个点的边的数量

连通图

概念：一个图中所有点之间至少存在一条路径（路径：一个点有一条路到达另一个点）的图

无向图：连通图

有向图

• 弱连通图：将此图转换为无向图后，是连通状态，即为若连通

• 强连通图：有向图中任意一点都存在一条到达其余所有点的路径

完全图

一张图中，任意两点之间均有着一条直接连接的边

树

概念：只有n-1(n:点的数量)条边的连通图

点和点之间的关系

• 父子
• 兄弟
• 祖孙

度：一个点的儿子数量

节点类型

• 根结点
• 分支节点
• 叶子节点

完全二叉树

概念：按照每一层节点依次填充的顺序的二叉树，是完全二叉树

特性：

• n层的二叉树，最多共有** 2n−12​n​−1个节点**
• 二叉树第n层，最多有个2n−12n**−1节点**

满二叉树

概念：n层的二叉树中所有分支节点的度数都为2

最小生成树

kruskal算法

#include<iostream>
#include<cmath>
#include<vector>
#include<algorithm>
using namespace std;
//kruskal算法 
const int N=2e5+7;
int n,m,p[N];
struct edge{
	int u,v,w;
	bool operator < (const edge t){
		return w<t.w;
	}
}edges[N];
int find(int x){
	if(p[x]!=x)p[x]=find(p[x]);
	return p[x];
}
bool merge(int a,int b){
	int fa=find(p[a]),fb=find(b);
	if(fa==fb)return false;
	p[fa]=fb;
	return true;
}
void kruskal(){
	sort(edges+1,edges+1+m);
	for(int i=1;i<=n;i++)p[i]=i;
	int sum=0;
	for(int i=1;i<=m;i++){
		int u=edges[i].u,v=edges[i].v,w=edges[i].w;
		if(merge(u,v)){
			sum+=w;
		}
	}
	cout<<sum<<endl;
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=m;i++){
		int u,v,w;
		cin>>u>>v>>w;
		edges[i]={u,v,w};
	}
	kruskal();
	return 0;
}

拓扑排序

//方法一
bool toposort() {
  vector<int> L;
  queue<int> S;
  for (int i = 1; i <= n; i++)
    if (in[i] == 0) S.push(i);
  while (!S.empty()) {
    int u = S.front();
    S.pop();
    L.push_back(u);
    for (auto v : G[u]) {
      if (--in[v] == 0) {
        S.push(v);
      }
    }
  }
  if (L.size() == n) {
    for (auto i : L) cout << i << ' ';
    return true;
  } else {
    return false;
  }
}
//方法二
#include<iostream>
#include<vector>
#include<queue>
#include<stack>
using namespace std;

int n,m;
int in[100005];
vector<int> vt[100005];
//int out[1000005];

int main(){
	cin>>n>>m;
	while(m--){
		int a,b;
		cin>>a>>b;
		vt[a].push_back(b);
		in[b]++;
		//out[b]++;
	}
    stack<int> stk;
    for(int i=1;i<=n;i++){
        if(in[i]==0) stk.push(i);
    }
    while(!stk.empty()){
        int p=stk.top();
        stk.pop();
        cout<<p<<" ";
        for(int i=0;i<vt[p].size();i++){
            int t=vt[p][i];//获取这条边的终点
            in[t]--;
            if(in[t]==0){
            	stk.push(t);
			}
        }
    }
	return 0;
}

迪杰斯特拉

struct edge {
  int v, w;
};

struct node {
  int dis, u;

  bool operator>(const node& a) const { return dis > a.dis; }
};

vector<edge> e[maxn];
int dis[maxn], vis[maxn];
priority_queue<node, vector<node>, greater<node> > q;

void dijkstra(int n, int s) {
  memset(dis, 0x3f, (n + 1) * sizeof(int));
  dis[s] = 0;
  q.push({0, s});
  while (!q.empty()) {
    int u = q.top().u;
    q.pop();
    if (vis[u]) continue;
    vis[u] = 1;
    for (auto ed : e[u]) {
      int v = ed.v, w = ed.w;
      if (dis[v] > dis[u] + w) {
        dis[v] = dis[u] + w;
        q.push({dis[v], v});
      }
    }
  }
}

位运算符

左移运算：<<

用法：** **x<<y

作用：将表示** x 的二进制数的每一位左移 **y 位，移出去的数就丢掉，空余地方用 0 补位。

例如：一个二进制数 10101011 将其左移 3 位，得到 01011000。

右移运算：>>

用法：x>>y

作用：将表示** x 的二进制数的每一位右移 **y 位，移出去的数就丢掉，空余地方用 0 补位。

例如：一个二进制数 10101011 将其右移 3 位，得到 00010101。

按位与运算：&

用法：x&y

作用：按位进行与运算。

例如：1101 和 0011 进行与运算就为：0001。

按位或运算: |

用法：x|y

作用：按位进行或运算。

例如：1101 和 0011 进行或运算就为：1111。

按位异或运算：^

用法：x^y

作用：按位进行异或运算。

例如：1101 和 0011 进行异或运算就为：0001。

按位非运算：~

用法：~x

作用：按位进行非运算。

例如：1101进行非运算就为：0010。

状态压缩常用位运算符技巧

1.取出x的第k位:

y = x&(1<<(k-1));//i<<(k-1)能够做成一个第k为1，其余位为0，如:10000 的二进制数，再结合位与运算就能提取到变量x的二进制中第k位数为1还是0了，常用于判断

2.将x第k位取反:

x ^= (1<<(k-1));//通过左移制作一个10000般的二进制数，然后结合异或运算的特点，将变量x的二进制中第k位数取反

3.将x第k位变为1：

x |= (1<<(k-1));//通过左移制作一个10000般的二进制数，然后结合异或运算的特点，将变量x的二进制中第k位数修改为1

4.将x第k位变为0：

x &= (~(1<<(k-1))); //通过左移制作一个0001 0000般的二进制数，然后位非运算将其修改为1110 0000般的二进制数，最后结合位与运算的特点，将变量x的二进制中第k位数修改为0

5.将x最靠右的1去掉：

x = x&(x-1); //减去1会将数字二进制中末尾的1去掉，然后需要借位的地方全变为1，如原1010 0000，减去1后变成1001 1111，再进位与运算得1000 0000，相当于去掉末尾1

6.取出x最靠右的1:

y = x&(-x); //结合负数的二进制的特点，如数字20的二进制为0001 0100，-20的二进制为1110 1100，再进行位与运算能够获取到二进制数100也就是4，及提前数字x中包含的最大2的指数值

7.判断是否有两个连续的一：

if(x&(x<<1)) cout<<"YES"; //左移后的数字会进行偏移，如13的二进制0000 1101，左移后未0001 1010，再进行位与运算，连续的1会在偏移后有至少一个1重叠，让结果不为0，如果结果为0，说明不存在连续的1

8.枚举子集：

for( int x = sta ; x ;  x = ( ( x - 1 )&sta) )  
	cout<<x;//通过技巧6的方式，如二进制:1011 0101,此循环能够枚举1011 0101、1011 0100、1011 0000、1010 0000、1000 0000这几个数据，即十进制：181、180、176、160、128这几个数字。

freopen("A.in","r",stdin); freopen("A.out","w",stdout);

深搜模板

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<map>
#include<deque>
using namespace std;

int n,m;
char mat[505][505];
int vis[505][505];
int dx[4]={1,0,-1,0};//下右上左 
int dy[4]={0,1,0,-1} ;
int flag=0;
void dfs(int x,int y){
	vis[x][y]=1;
	if(mat[x][y]=='g'){
		flag=1;
		return;
	}
	for(int i=0;i<4;i++){
		int tx=dx[i]+x;
		int ty=dy[i]+y;
		if(mat[tx][ty]=='#') continue;
		if(vis[tx][ty]==1) continue;
		if(tx<1||tx>n||ty<1||ty>m) continue;
		dfs(tx,ty);
	} 
}

int main(){
	cin>>n>>m;
	int a,b;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cin>>mat[i][j];
			if(mat[i][j]=='s'){
				a=i,b=j;
			}
		}
	}
	dfs(a,b);
	if(flag) cout<<"Yes";
	else cout<<"No";
	return 0;
}

GESP二级考点

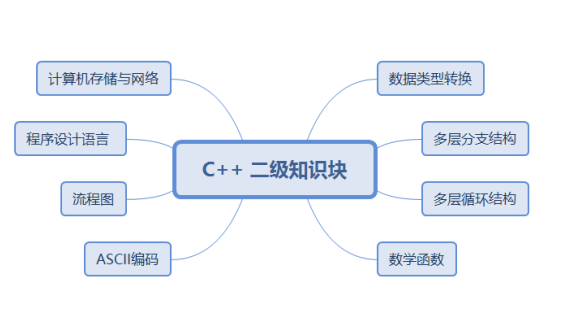
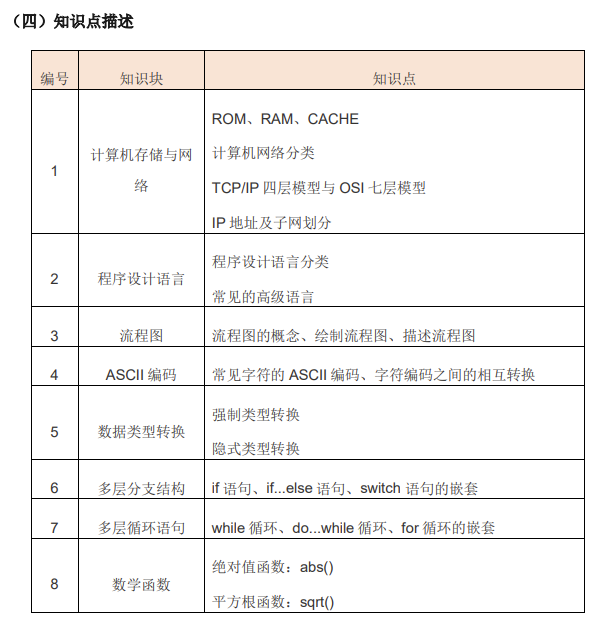
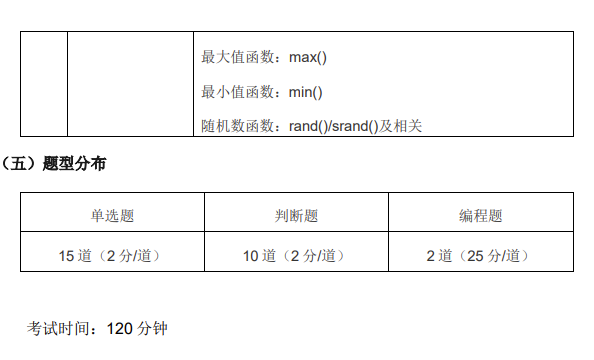
GESP三级考点

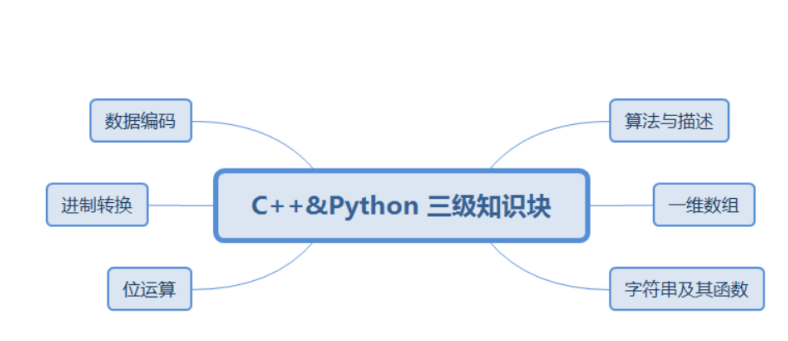
GWL要吃郑兴亚，害怕ing......

主域一言

没有任何人有资格剥夺他人的愿望，即便是「神」也不行。

神在白天做梦，太阳在西边升起。

如果有个你喜欢的女孩子，可千万不要凶她哦

不要随便对女生做承诺,尤其是在你没有把握的情况下。

能够被人们正常理解的现实，只是大概率事件恰巧发生了而已。

错误可不是为了别人才改的过来的，要为了自己才能改正。

如果命运扼住了你的喉咙，那你就挠命运的胳肢窝。

每个生灵的意志都值得被尊重，就像海中的游鱼，也有自己的方向。

你才是⑨！你全家都是⑨！

此时此刻的咱啊，能和汝在一起，是最幸福的了。

这个社会一直在淘汰有学历的人，但是不会淘汰有学习力的人。

如果我们只看到自己的普通，可能就会错过特别的人生。

今后无论发生什么事也好，这个左手上的⋯⋯都是同伴的记号！

愿你的青春如花般绽放。

如果你一个人把什么都做完了，那我做什么？

凡是过往，皆为序章

我们终将上岸，阳光万里

静下来想你，一切都美好的不可思议

再等等，山南水北，我一定陪你去

你种的花，人间早就开遍了

一小片夕阳落在我手上

善良并不是软弱，温柔并不是妥协，在这个嘈杂的世界中，不慌不忙地成长

相知无距，雁回千里书须寄。

总之岁月漫长，然而值得等待

历经万般红尘劫，犹如凉风轻拂面

把酒祝东风，且共从容

一生温暖纯良，不舍爱与自由

落花人独立，微雨燕双飞

夜月一帘幽梦，春风十里柔情

连天衰草，望断归来路

所有晦暗都留给过往，从遇见你开始，凛冬散尽，星河长明

我已经不再什么事都拜托星星了

希望我们都在各自的未来里闪闪发光

不该这样 又好像 只能这样

不刻意讨好，也会有人来爱你 ​​​

你别着急长成一个正确而无趣的大人

让我掉进你的梦里吧

不要被这个世界所改变

我们也是光亮本身

温柔的人像一片沼泽

想握住此生辽阔，赠你漫天星火

很想带你去吹吹风

你未必光芒万丈，但始终温暖有光

我希望你是无忧无虑的风

我的耐心与偏爱都是为你准备

邀一夜星河 去你梦里做客

人会因为嘴硬失去很多东西吧 ​​​

脚踏实地 才能摘到星星揽到月亮 ​​​

喜欢一定宛如大海

会晚些 但会更好些 ​​​

一切尽意 百事从欢

星星不该为毁星者消耗光芒

活在当下，只需愉悦

逃离任何消耗你快乐的东西。

圣经说:别惊动我爱的人 等他自己情愿

漫天繁星中总有一颗属于你

你终会是一个人宇宙限量贩售的快乐

努力的尽头一定要是你，拜托了

总之岁月漫长，然而值得等待

愿你流浪半生 归来仍是少年

我看见白日梦的尽头是你

一切都会变好 过了黎明就破晓

对的那条路，还是有些曲折的

来日纵是千千晚星

不闻星河须臾固执走向你

​​​再辛苦也要忍耐等待时机

放弃不难，但坚持一定很酷

​只要活着，就已经是最大的正能量

岁月漫长 要心地善良

星光不问赶路人，时光不负有心人

想用最初的心 陪你走最远的路

既见君子，云胡不喜

愿我所爱，平安顺遂

好好生活 总会遇见美好的事

​​万物不及你眉眼

为见公子 千里迢迢

如果人人都理解你 那你岂不是太普通了

你就是这世间最好的期待与惊喜

白白胖胖 充满希望 ​​​

不争 不让 事不过三 ​​​

你值得一切好的东西 包括被爱被珍惜 ​

我的宇宙里为你藏有无数个温柔星球

肩膀有点痒 可能要长小翅膀 ​​​

请你全力以赴去开心

对未来的真正热爱 是把一切献给现在

希望你的底色一直是善良和勇敢 ​

想借你心头的月亮乘进一片浪漫 ​​​

愿我们在彼此看不到的岁月里熠熠生辉 ​​​

迷人且温柔 知进且优秀 ​​​

躲起来的星星也在努力发光呢 ​​​

有生之年，欣喜相逢

幸与不幸都有尽头

努力会让你不需要魔法也拥有奇迹。 ​​

听风与凤窃语 看漫天熠熠星辰

我不是光芒万丈，但是也在努力发光

星光璀璨不及你

你有没有这种感觉，好像一生都身不由己

你是我年复一年，藏在枕下的春秋大梦

当太阳升起时 就该把昨天忘掉 ​​​

等到适合的时间我们再相遇

今天也要努力维护世界和平

想认真的生活，不负任何人

夜晚潮湿 地面潮湿 空气寂静 树林沉默

想要成为能带给别人温暖的那种人

巨鲸落，万物生

拥抱的最好定义，是交换温柔啊

正因为不完美，我们正在努力变完美

如果你的心简单，那么这个世界也就简单

一切从上帝开始，最后仍归于上帝

“人间烟火气，最抚凡人心”

如今我与岁月山河同好

因为乌鸦像写字台

所有努力，是为了让自己也有光芒

你头发乱了喔

大家都要努力生活哇

如果你热爱生活 生活一定比谁都清楚

你们是永不落幕的深海星辰

我们都要平平安安的携手同行

少年之诚，足以消弭戾气

愿我所爱，平安顺遂

喜欢过很多很多

我喜欢阳光照射盛树投影出斑驳交错

我喜欢海风吹鼓帆船渐行消失天际

我喜欢大雨后街道尽头夕阳西下

我喜欢寂静半夜火车悠扬鸣笛

我喜欢夏天穿过脚踝那晚风

我喜欢古色古香旧巷城楼

我喜欢冷清店铺慢音乐

我喜欢旷野上的马路

我喜欢书配杯热茶

我喜欢繁星低沉

我喜欢邓紫棋

我喜欢自由

我喜欢风

角色语录

死亡不是生命的终点，遗忘才是

人生仅有一次的绝景

生命就像人家的魔法书~涂涂改改又是一年！

知识就是力量

一不小心就干掉了个大家伙！

哟吼~火烧屁屁咯~

我很生气，后果很严重

玩火~自焚~

萝莉身~御姐心

干掉他们！

魔法，为我而存在。

吊车尾的家伙们，羞羞羞~

点燃你们，就有烟火看咯！

Bingo，人家就是来砸场子的！

神秘，会屈从于更高的神秘。

替你点跟蜡~

一直都赢，也挺无聊

斩草除根！

一个人，没有同类

我为黑暗服务。

虚无，是我的信条！

刀鞘，丢失了。

所谓武技，不过是遇害者数字的累积而已。

好奇心的代价，很昂贵

不逃，就不会死。

补刀的时刻。

收割开始

替你的生命倒数

刀锋所划之地，便是疆土

终究，堕入深渊

了无遗憾地离开吧！

连续讨伐！

今天出门前拜过主宰，以及峡谷野生动物吗?

最成功的狩猎者，猎取的可不仅仅是龙

猫车说走就走

记住，玫瑰有刺

放下剑！去找别的活法。

能够不流血而胜利，是最完美的胜利。

使命常与剑相伴

美丽的事物，总是很棘手

保持分寸。

已显现的命运，不会因逃避而改变。

远离那些……只凭狂想的艺术和笃信杀戮的战斗。

我们珍视荣誉，但绝非过去的荣誉。

神不会对胆小鬼微笑。

光明会将我们引向同一个终点。

站起来!这样就不行了?

还算配得上我的对手~

要放你逃跑吗?

我竟然会失败…...!

可渡为劫，弗渡为命?

销骨熔金，不灭我心。

我胜造化一执念!

天赋九尾，舍之无悔!

一梦心期一千劫……

当日天火骤至，青丘十方成灰……不知族亲今日可还安好?

明焰九转炼心魄，遍踏劫灰始归来。

族中长辈说过，世上最凶残的大妖，叫做“命运无常”

话本里的狐妖故事几分真，几分假?凡人莫要全信。

听说人和妖一样，都喜欢把本相藏起来。

故里青丘，处东海之外，乃红尘之都，庇佑周天狐族。

能解一族之祸，形神俱灭又如何!

兄长曾说，我们狐族至宝内藏乾坤，可助凝神固灵……

在梦里，姐姐们向我招手……她们，要去哪里?

镜子所能折射的，是我心中的太阳。 如幻如镜，如影随形！心有暖阳，万丈光芒！

镜花水月皆是梦幻泡影，心有暖阳成就万丈光芒！

所有光影都是虚幻的，唯有金钱才是硬道理。

照镜如水，见面之容！

深入敌军有何难，一人当抵百万兵。

似山涧清泉，清澈见底，一览无遗。

我不当别人的影子，每一片镜子里都有阳光。

没有谁是谁的影子，镜中镜外，都是我们自己。

这世上有很多奇迹，而我，不止奇迹

你可以飞得很高，但我还是你姐姐

阴影笼罩大地，而太阳将刺穿黑暗。

我喜欢绝望的感觉，置之死地，必有后生。

以无止之神，行有止之境

怀八荒，入九重——日月安属，列星安陈！

在真正的光明到来前，成为太阳之力的接引者，焕发炙热火光。

光明的心愿，走上不可预知的前路。

从逆境中寻找绝无仅有的生机，是深渊在后力战不退下的一线希冀。

把登临绝顶的赛场称作奇迹，把逆转大局奠定胜利的战斗称作奇迹。

花如盛世绽放，以人心培育。

心似时光飘零，以生命愉悦。

乾卦，飞龙在天，宜上分。

明夷，晦暗之象，顺风当慎行。

无妄，天命不佑，小心队友。

复卦，万物亨通，逆境可再兴。

命运会否与卦象如一，拭目以待吧。

一堆无用的热情。

失去的便应当取回，这没有错。

我的就是我的，终究属于我的。

血管里，流淌着忘川之水。

长安和亲人，选哪一个。

若牵挂的人只存在回忆中，才是彻头彻尾的失败。

真是算过的卦里最烂的八字。

离卦，上九，宜征伐。

蝴蝶是我，我就是蝴蝶

梦到了传奇的世界，还和奔波儿灞打了声招呼。

你在做梦，哼！就是那个做梦的做梦

美妙的长眠，值得高歌一曲，啦

一群人在人家梦里打来打去，有意思吗？

天地与我并生，万物与我为一。

梦里花落知多少。

美梦成真。

其实，刚才说的全是梦话。

醒醒吧，少年。

最近脑洞太大，得补补

我的坐骑可是纯天然无污染。

撼天地，镇乾坤

嵩山如卧，万物一府

一朝入梦，八极恣游

浮云之上，九天之外，便是吾乡所在

人非草木，安知草木无情?

长眠是种介于生死间的奇妙境界

鲲说，无需害怕，因为它在这里

鲲说，它愿以微薄身躯，换得一山生灵

我，别无所求……

玄山妙水，见而忘忧

生亦何欢，死亦何苦

知道什么是无用之用吗

会原谅我的任性吗？

守望着天空，大海和你的回忆。

完美，是最无情的禁锢！

空洞和孤独，是依靠温暖的灯光填补。

潮水中，沉默着被遗忘的名字，他们隶属于自作多情的泡沫！

映照潮汐的起伏，以免迷失战场的道路。

点亮的星，不会轻易熄灭！

破碎的奇迹好过没有，苦恼的希望胜于迷惘。

魔道的天才们属于同一种流派，偶像派。

前往需要你的地方。

会原谅，我的任性吗？

守护爱人的心，因恐惧失去而污秽。

看不见的那只眼里，有你不该看见的过去。

人生，就是不断的战斗。

想挑战的排好队，一个一个来!

太无敌而找不到对手，也是种无敌的忧伤!

在非人的领域，也同样无敌!

无敌的我，又迷路了。

修行之路，永无止境!

浪迹天下，未尝一败!

武士的灵魂，可是比心脏更重要的东西!

没有一往无前的觉悟，就不配握紧手中的双刀!

朝一个方向走下去，便总有相见的那天。

最有价值之物，给最珍贵之人 有珍宝，不如有眼光

速战速决

今夜三更过后，你的手办尽数归我

少女怎么会拒绝闪耀的宝藏呢

啊，你的命看起来没什么收藏价值

最喜欢的是西施姐姐，还是夷光姐姐

大鱼，我们好像在哪见过

奇珍异玩大多低调，花哨的外表光会骗人

东施效颦

来抓我呀，笨蛋

每一种境遇，都是命运的附赠品

看，飞碟

有家人的地方，就是家

最佳组合，勇气、实力，再加一些小小的花招

生活像一张蜘蛛网，我的日常，就是钻它的空子

闪闪发光的队长，你好

说好了，人头归你，水晶归我

纷纷吹落无尘处……霜雪澄明，冰心可鉴。

砺雪凌霜三尺剑，为示天下不平人。

剑指千星，问道苍冥。

雪境化三清域外，寸心系尘世万千。

修真者的仙途，何以由凡人的牺牲铸就?

未曾被上苍注视的生命，亦将名姓写在天地之间。

荒原上终年不化的冻雪，是飘零之魂的凝结。

他们的呼声，遗落为深谷中冗长的回音。

众生决意即为剑意，万世民心可证道心。

活下去……为了和我们一样的漂泊者，不再别离。

怎能...在此刻离去……

风骨尽失，仙道何存?

空山无归，春风不渡。

苍风试霜刃，冷月照归人。

烈阳终有不及处，人心如渊壑。

红月正当空，逢魔涤荡，归途迷雾中。

日光穿透睡蝴蝶，树影婆娑间。

听，神铃千重，故国永续传说中。

世如朝露又奈何。

破晓之曦！

燃心之焰！

日曜之羽！

日影人声今何地？风透鸟居，归来亦寻觅。

出云！

神照！

也逢黄昏也逢晨!

日高晴暖！

月因情生，月之情有谁复知？

君亦失路之人？

谢谢你，玛玛哈哈。

来吧站起来。

这是来自大自然的惩罚。

接受自然的报应吧。

我们走玛玛哈哈。

这样如何呢？

风之刃。

天空之牙。

感受自然的痛楚吧。

没人能在喵的暴躁节奏里战胜本猫。

长城之子，归于长城。

今天的本猫，自然是易燃易爆炸的喵。

本猫守望的长城，屹立不倒

一硫二硝三木炭，解构你轰轰烈烈的人生

爆炸就像孤独，不是你想停，想停就能停。

让本猫示范下，动口又动手的输出

即便三分钟热度，也足以穿透次元壁

制造真正的爆款

保护我方队喵

定义下震撼两个字

又多了个哑炮，喵喵喵

崩塌的不止防御塔，还有你最后的倔强

人有人设，猫当然有猫设，维持猫设很重要的

勇士之地也存在吸猫势力吗

不接受对立物种的投喂，乃基本尊严。。。真香。。

能打能扛能热锅，恩。值得深入拆解

第一百二十八次拆解，失败...

太古有士，姓薛名定谔，为云中漠地猫系混血魔种的先祖

没有好好研究过猫奴的自我修养，怎么养我?

冤冤相报何时了，要善良~

放下仇恨的小本本，否则很容易长皱纹。

有文化的人，连撸猫都更有范

太软弱的人，会被炸成天边的烟花，尸骨无存

队长，率领我们冲锋吧，本猫很清楚，什么是值得做的事

如果不能给女孩子留下好印象，那么留下表情包也是可以的

方士，你寻求到了吗?梦寐以求的幸福

停止你对哥哥的炫耀，嫉妒另本猫提前引爆。

失败者连喵都没的撸

听过那个传说吗?抛弃长城的人会一去不返。

惨无人道的猫薄荷投喂。。真。香。。

你失败的这片地盘，都由本猫承包了

神在白天做梦，太阳从西边升起。

过去生于未来。

羁绊无影无踪，藤蔓一斩就断。

什么小鹿女啊，一定是世界上最不可爱的孩子吧。

云梦泽没有东边和西边。

你为什么粘着我呀。

看，空气。

有的神住在天上，有的神住在蘑菇里。

要把梦藏在树叶里，不然梦会坏。

我们从玄微森林出来的人，一天要吃掉半个大陆呢。

昨晚我偷了你的翅膀，在天上玩了一圈。

不是我，真的不是我。

别难过，我只是睡一觉。

这是谁的小鹿，真厉害。

别赖着人家好吗。

阿瑶为你痛哭。

我已经洗过脸了，真的。

狼来啦！

你好，小鹿（东皇太一），你好，小蛇（瑶）

阿瑶也想成为，像老师一样高大的人。

万物有灵，生生不息。

神在白天做梦，太阳从西边升起。(主域一言孩子们）

要变成光，因为有怕黑的人。

由画而生，随心而为。

嗯~，想起了很久很久以前的故事。

喂，你就是我在等的人吗？

下次还要来陪我啊。

你从哪处世界来？（杨玉环）峡谷西边数，第二朵蓝色的花。我从那里来？（瑶）

除了我以外，好看的人都从云上来

啊，峡谷还是要靠我来守护

这里以前光秃秃的

嗯，想起了很久很久以前的故事。

喂，你就是我要等的人吗。

下次还要来陪 我呀。

你从哪处世界来？峡谷西边数，第二朵蓝色的花，我从那里来。

除了我以外，好看的人都从云上来。

唉，峡谷还是要靠我来守护。

呃，这里以前光秃秃的。

等我很久了吧。

哎，你也是来找小鹿的呀。

嘘，别说话。

啊，没见过什么小鹿呀。

呀，有一头会开花的鹿。

你在看哪

月牙泉，昨晚被我喝光了!

听，沙子在唱歌。

诶，我也会飞了。

这棵树比天还高，你猜猜是谁种的。

我会换一种方式陪着你。

想去云的另一端看看吗。

树林是红色，小山是绿色，你猜小鹿是什么颜色。

由画而生，随心而为。

万物有灵，生生不息。

要变成光，因为，有怕黑的人。

飞舞战场的美少女，大活跃Q

左三圈，右三圈，扭一扭，转一转……人家也是萝莉控

出发喽，蹂躏脑筋不好的老年人

心有多大，舞台就有多刺激

男神是孟德大人，喜欢的宠物是阿典，梦想是养只羊驼

呜~少女心破碎了

宝宝不开心，宝宝有小情绪

颜值不够，又不听话，哼，告诉你家长呦

1逗~~你~~玩~~~~

大人，是种邪恶可怕爱说谎的生物，哼

做个狂热又任性的魔女，把帅气的男朋友带回家~

虐虐更健康(S9赛季新增)

人家演奏，大家都加油（S9赛季新增）

不要欺负我，我会把你弄哭的哟~

吟诵十四行诗，作为仲夏之梦的开场

月光下邂逅的，是你，或者爱情?

好好欣赏吧，莎士比亚曾游历过的花园

星光化作翅膀，长久闪烁

明月装饰了你的窗户，你装饰了我的梦境

纵使魔法遮蔽了眼睛，心灵依然指引着爱情。

真爱之路，从无坦途

时间带不走美妙的青春，他被珍藏于仲夏夜的诗篇。

夏日，凋零……

呵呵，夏日和我，谁更可爱?

啊，你在哪，我好害怕。

为什么爱情，不能传染。

禁止亵渎爱情!

关于玫瑰和谎言的游戏，你输了~

霓为衣兮霞为裳，蜃楼起兮海雾茫……前梦宛然，去者犹在。

呵云气兮成万象，筑高台兮凌穹苍……月照天门，蜃境始开。

天上宫阙无处归……莫回首，梦觉已千秋。

梦中有人间，海上有云烟。

“船过沧浪，骤起蜃楼;客行广漠，忽现海市……”这就是凡世中，关于我们的记述?

见过万物易碎，就见过了我。

比月华兮短年光，比昙华兮朝暮亡……

他人笑尔频说梦，(轻笑)焉知彼亦非梦中?

愚人一做梦，他者遍体鳞伤。

似假似幻，非雾非烟～

从来好物不坚牢，彩云易散琉璃碎。

让故人魂梦，不再四处漂泊。

都化作，片羽浮光……凡所有相，皆是虚妄。

若非痴人，何以说梦?

天人栩栩来～

魂牵旧影～

斯人出没水云间。

氤氲蜃气，吁成天阙～

蜃楼如故，昨梦已非……

千年旧影，筑作刹那绮境!

景色如旧，何须再三观赏?

水中捞月，徒然而已。

剪明月为蚀，戴天穹之上。

珠宫贝阙，一如当年。

重到旧时蜃气楼～

看取繁华几千重。

世情多变幻，流水迢无返。

妄念起，罪孽生。

幽昙梦短，月明他乡。

未竟之舞，不可再得。

牵云以为衣，曳露举作佩。

让我看看是哪个小可爱这么无聊没写完代码在看别人主页看到底的鸭~~，赶紧去写代码！！！啊哈哈哈哈哈哈哈哈哈哈哈哈哈哈啊哈哈哈哈哈哈哈哈哈哈哈啊哈哈哈哈哈哈哈哈，姬霓肽鋂