- 题解
西川中学 - CSP 专项训练
- @ 2025-3-26 13:27:48
洛谷网站:https://www.luogu.com.cn/ 请注册账号,记住账号和密码
T2 知识点和训练
二、质数的筛选法
质数筛也叫素数筛,是求1到n之内素数的优化算法,质数筛有两种,埃氏筛和欧拉筛。
1.暴力枚举
 模板代码示例
模板代码示例
#include <bits/stdc++.h>
using namespace std;
//判断素数
bool prime(int val){
// 1-3的值需要特判,因为我们循环判断只判断到sqrt(val),1-3是判断不了的
if(val==1)return 0;
if(val==2||val==3)return 1;
// 为什么只要判断到sqrt(val)?
// 例如一个数8,它的因数有1、2、4、8,可以发现1<2<sqrt(8)<4<8
// 所以我们只要判断小于sqrt(8)的数就可以了,因为因数都是成对出现的
for(int i=2;i<=sqrt(val);i++){
// 如果被整除了,那么该数一定不是素数,返回0
if(val%i==0)return 0;
}
// 如果是素数就返回1
return 1;
}
int main(){
int n;
cin>>n;
for(int i=2;i<=n;i++){
// 如果返回值是1,那么该数是素数,输出即可
if(prime(i)==1){
cout<<i<<' ';
}
}
}
2.埃氏筛

#include <bits/stdc++.h>
using namespace std;
int main(){
// f[i]=1代表i不是素数,f[i]=0代表i是素数
int f[100010]={1,1};
int n;
cin>>n;
// 埃氏筛
for(int i=2;i<=n;i++){
if(f[i]==1)continue;
for(int j=2;i*j<=n;j++){
f[i*j]=1;
}
}
// 打印
for(int i=0;i<=n;i++){
if(f[i]==0){
cout<<i<<' ';
}
}
}
3.欧拉筛

#include <bits/stdc++.h>
using namespace std;
int main() {
int d = 0; // 质数计数器,记录已找到的质数数量
int p[100010] = {0}; // 存储质数的数组
int f[100010] = {1, 1}; // 标记数组,f[i]=1 表示 i 不是质数,f[i]=0 表示 i 是质数或未标记
int n;
cin >> n; // 输入正整数 n,表示寻找 1 到 n 的质数
// 埃氏筛法:生成 2 到 n 的所有质数
for (int i = 2; i <= n; i++) {
if (f[i] == 0) { // 如果 f[i] 未被标记,说明 i 是质数
p[d++] = i; // 将质数 i 存入 p 数组,d 增加
}
// 使用已找到的质数 p[j] 标记 i 的倍数为非质数
for (int j = 0; j < d; j++) {
if (p[j] * i <= n) { // 如果 p[j] * i 在范围内,标记 p[j] * i 为非质数
f[p[j] * i] = 1; // 标记 p[j] * i 为非质数
} else {
break; // 如果 p[j] * i 超过 n,后续的 p[j] 更大,无需继续,退出内层循环
}
if (i % p[j] == 0) { // 如果 p[j] 是 i 的因数
break; // 后续的质数 p[j+1] 等无需继续检查,退出内层循环
// 因为 i 的更大因数对应的倍数会在后续 i 的迭代中处理
}
}
}
// 输出 1 到 n 的所有质数
for (int i = 0; i < d; i++) {
cout << p[i] << ' '; // 打印质数数组中的每个质数,空格分隔
}
}

第 1 题:
#821. 质数筛选
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/821
第 2 题:
#T217. 【例36.3】 最大质数
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/T217
第 3 题:
#1373. 希蒙的质数和与积
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/1373
一、前缀和与差分
1.前缀和: 数组 d[i] 的对应的前缀和为:d[0] + d[1] + ··· + d[i] ;
假设数组 d[5] = [ 1, 3, 4, 6, 9 ],该数组的前缀和数组 prefixSum[5] = [ 1, 4, 8, 14, 23] ;
关键代码:
1)s[i] = s[i-1] + a[i]; // 计算前缀和
2)cout << s[r] - s[l-1] << endl; // 区间和
2. 差分数组: 数组 d 对应的差分数组的第 i 个元素 diff[i] = d[i] - d[i-1],(i > 0, diff[0] = d[0]) ;
假设数组 d[5] = [ 1, 3, 4, 6, 9 ] ,该数组对应的差分数组 diff[5] = [ 1, 2, 1, 2, 3 ] ;
关键代码:
1)d[i] = a[i] - a[i-1]; // 构造差分数组
2)d[l] += k; // 区间 [l, r] 起始处加 k d[r+1] -= k; // 区间 [r+1, n] 减 k
3)a[i] = a[i-1] + d[i]; // a[i] = d[1] + ... + d[i] // 通过差分数组前缀和恢复原数组
前缀和与差分数组一般是结合起来应用的;原数组、前缀和数组、差分数组,三者可以互相转换;一般是给一个初始数组,然后根据题目条件结合数组特点、规律,利用前缀和或差分数组求解题目;
规律、性质:
对于前缀和数组,原始数组中的第 i 个元素的变化(加、减等数学运算)都会影响到前缀和数组中第 i 个元素之后的所有元素;
一般应用:
对数组中某个区间上的每个元素加上或减去同一数值; 对数组中某个区间上的每个元素进行累加、累减、累积等操作;
第 1 题:
#904. 【模板】前缀和
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/904
第 2 题:
#897. 惆怅的希蒙
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/897
第 3 题:
#1090. 【模板】差分
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/1090
第 4 题:
#1790. 差分求和
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/1790
T1 知识点和训练
第 7 题:
#680. [CSP-J 2017] 成绩
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/680
第 6 题:
#664. [CSP-J 2018] 标题统计
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/664
第 5 题:
#1856. [CSP-J 2023] 小苹果
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/1856
第 4 题:
#969. [CSP-J 2022] 乘方
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/969
第 3 题:
#968. [CSP-J2021] 分糖果
题目链接: https://ac.xiaosaima.com/d/CD01_2404/p/968
第 2 题:
#282. [CSP-J2019] 数字游戏
题目链接:https://ac.xiaosaima.com/d/CD01_2404/p/282
第 1 题:
#967. [CSP-J2020] 优秀的拆分
题目链接:https://ac.xiaosaima.com/d/CD01_2404/p/967
CSP-J 知识点和思维导图
(在题库中进行搜索知识点进行自我练习)

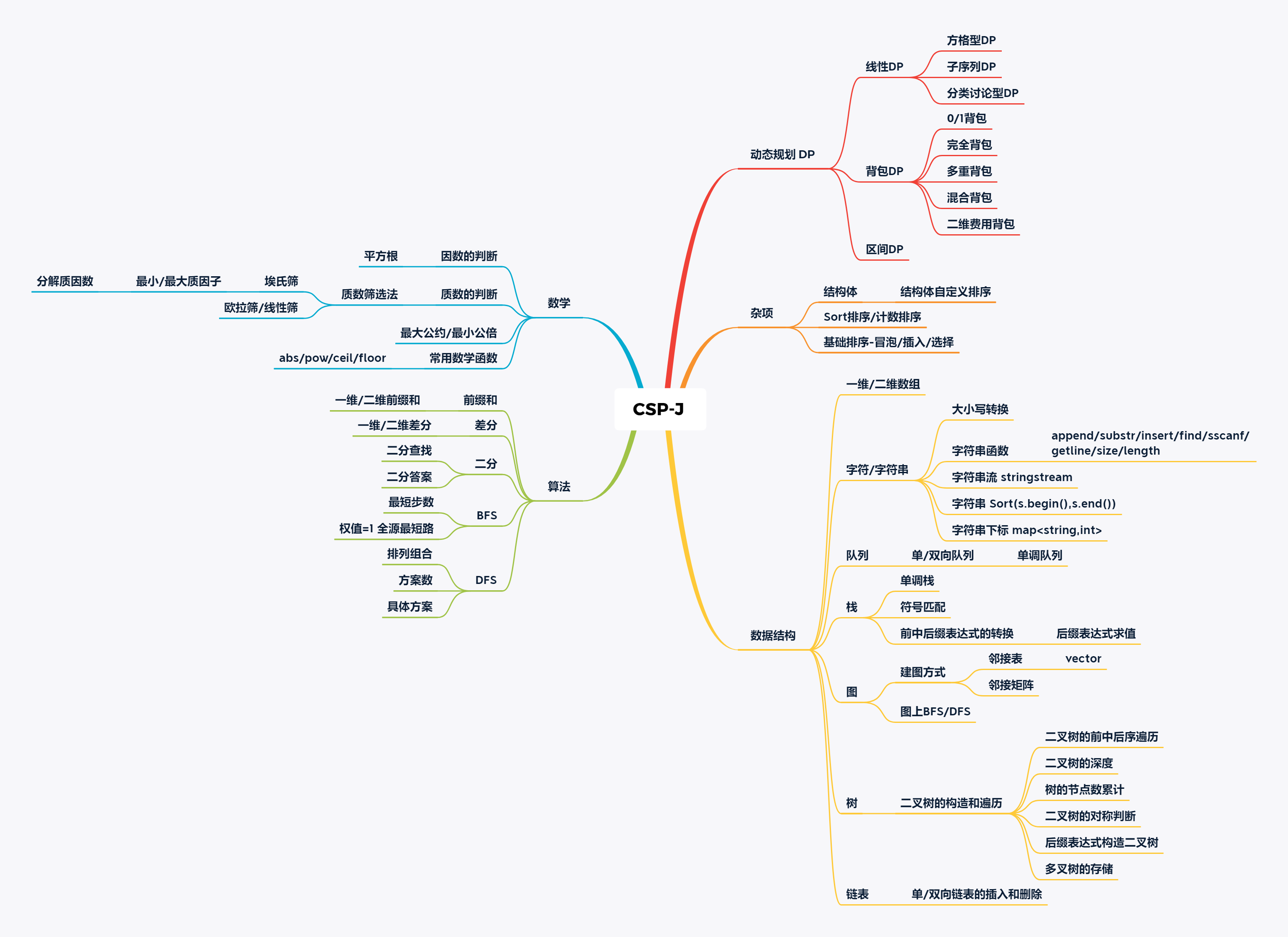
CSP-J历年考试题目:
2024年:T1-扑克牌、T2-地图探险、T3-小木棍、T4-接龙
2023年:T1-小苹果、T2-公路、T3-一元二次方程、T4-旅游巴士
2022年:T1-乘方、T2-解密、T3-上升点阵、T4-逻辑表达式
2021年:T1-分糖果、T2-插入排序、T3-网络连接、T4-小熊的果篮
2020年:T1-优秀的拆分、T2-直播获奖、T3-表达式、T4-方格取数
2019年:T1-数字游戏、T2-公交换乘、T3-纪念品、T4-加工零件
2018年:T1-标题统计、T2-龙虎斗、T3-摆渡车、T4-对称二叉树
2017年:T1-成绩、T2-图书管理员、T3-棋盘、T4-跳房子
2016年:T1-买铅笔、T2-回文日期、T3-海港、T4-魔法阵
2015年:T1-金币、T2-扫雷游戏、T3-求和、T4-推销员
2014年:T1-珠心算测验、T2-比例简化、T3-螺旋矩阵、T4-子矩阵
2013年:T1-计数问题、T2-表达式求值、T3-小朋友的数字、T4-车站分级
2012年:T1-质因数分解、T2-寻宝、T3-摆花、T4-文化之旅
2011年:T1-数字反转、T2-统计单词数、T3-瑞士轮、T4-表达式的值
2010年:T1-数字统计、T2-接水问题、T3-导弹拦截、T4-三国游戏
13 条评论
-
hishuchao LV 4 MOD @ 2025-5-12 10:07:49已修改
T2 知识点和训练
第 4 题:差分求和 公式推导:



第 4 题:差分求和 答案:
方法:差分公式
#include <bits/stdc++.h> using namespace std; int main() { int n; cin >> n; int a[500000]; for (int i = 0; i < n; ++i) cin >> a[i]; long long total_diff = 0; // 用于存储所有差值的总和 long long prefix_sum = 0; // 前缀和,用于记录数组元素从开始到当前位置的累加和 long long first_diff = 0; // 存储第一个差值(即 a[1] - a[0]) for (long long j = 0; j < n; ++j) { if (j > 0) { // 计算当前差值:a[j] * j - prefix_sum,a[j] * j 表示当前元素 a[j] 在位置 j 的加权值,prefix_sum 是前 j-1 个元素的累加和 long long current_diff = a[j] * j - prefix_sum; total_diff += current_diff; // 将当前差值累加到总差值中 if (j == 1) { first_diff = a[j] - a[j - 1]; // 当 j == 1 时,计算第一个差值 a[1] - a[0] } } prefix_sum += a[j]; // 更新前缀和,加入当前元素 a[j] } // 计算最终结果:第一个差值减去 (总差值 - 第一个差值) // 相当于 2 * first_diff - total_diff long long result = first_diff - (total_diff - first_diff); cout << result << endl; return 0; } -
@ 2025-5-12 9:59:30
T2 知识点和训练
第 3 题:【模板】差分 答案:
方法:差分公式
#include <bits/stdc++.h> using namespace std; int main() { long long a[100005], d[100005]; int n, m; cin >> n >> m; for (int i = 1; i <= n; ++i) { cin >> a[i]; // 读取初始数组并初始化差分数组 d[i] = a[i] - a[i-1]; // 构造差分数组 } while (m--) { // 处理 m 次操作 int l, r; long long k; cin >> l >> r >> k; d[l] += k; // 区间 [l, r] 起始处加 k d[r+1] -= k; // 区间 [r+1, n] 减 k 可以理解为公交车上下乘客 } for (int i = 1; i <= n; ++i) { // 通过差分数组前缀和恢复原数组 a[i] = a[i-1] + d[i]; // a[i] = d[1] + ... + d[i] cout << a[i] << " "; // 输出结果 } return 0; } -
@ 2025-5-12 9:54:15
T2 知识点和训练
第 2 题:惆怅的希蒙 答案:
方法:前缀和公式
#include <bits/stdc++.h> using namespace std; int main() { int n, m; cin >> n >> m; if (m == 0) {// 特殊情况:m = 0 cout << 0 << endl; return 0; } int a[3000001]; // 根据题目最大 n = 3*10^6 for (int i = 0; i < n; ++i) { cin >> a[i]; } long long sum = 0; for (int i = 0; i < m; ++i) {// 计算第一个窗口的和 sum += a[i]; } long long min_sum = sum; // 初始化最小值 for (int i = m; i < n; ++i) { sum = sum - a[i - m] + a[i]; //滑动窗口,减去窗口左端,加上右端 if (sum < min_sum) { min_sum = sum; // 更新最小值 } } cout << min_sum << endl; return 0; } -
@ 2025-5-12 9:50:19
T2 知识点和训练
第 1 题:【模板】前缀和 答案:
方法:前缀和公式
#include <bits/stdc++.h> using namespace std; int main() { int n, q; cin >> n >> q; long long a[100001], s[100001]; // n <= 10^5 s[0] = 0; // 前缀和边界 for (int i = 1; i <= n; ++i) { cin >> a[i]; s[i] = s[i-1] + a[i]; // 计算前缀和 } while (q--) { // 处理 q 次查询,用for循环也OK int l, r; cin >> l >> r; cout << s[r] - s[l-1] << endl; // 区间和 } return 0; } -
@ 2025-5-7 13:25:42
#include<bits/stdc++.h> using namespace std; int main() { int n,m; int a[100005]; cin>>n>>m; for(int i=0;i<n;++i){ cin>>a[i]; } if(m==0){ cout<<0<<endl; return 0; } long long nowsum=0; for(int i=0;i<m;++i){ nowsum+=a[i]; } long long minsum=nowsum; for(int i=m;i<n;++i) { nowsum=nowsum+a[i]-a[i-m]; if(nowsum<minsum){ minsum=nowsum; } } cout<<minsum<<endl; return 0; }👎 1 -
@ 2025-4-30 8:54:39
T1 知识点和训练
第 7 题:参考讲解和答案:
方法:数学
#include <bits/stdc++.h> using namespace std; int main() { int a, b, c; cin >> a >> b >> c; cout << 0.2 * a + 0.3 * b + 0.5 * c; return 0; } -
@ 2025-4-30 8:46:08
T1 知识点和训练
第 6 题:参考讲解和答案:
方法1:遍历统计
#include<bits/stdc++.h> using namespace std; int main(){ int cnt = 0; string s; getline(cin, s); // 读取一行输入的字符串(包括空格) for(int i = 0; i < s.size(); i++){ // 遍历字符串的每个字符 if(s[i] == ' '){ continue; } else{ cnt++; } } cout << cnt; return 0; } -
@ 2025-4-21 10:18:43
T1 知识点和训练
第 5 题:参考讲解和答案:
方法1:循环模拟
#include <bits/stdc++.h> using namespace std; int main() { int n,t=0,id=0;//n个苹果,t代表所需的天数,id代表拿走编号为 n的苹果是在第几天 cin>>n; while(n){ t++; //第t轮取苹果 if(n%3==1 && !id) id=t; //n被独立分组且最后一个苹果尚未取走,这时的 t是答案 n=n-((n+2)/3); //每次被拿走 n的1/3,(n+2)/3为 n除以3向上取整 } cout<<t<<" "<<id; return 0; }👎 3😄 1 -
@ 2025-4-16 12:32:14
T1 知识点和训练
第 4 题:参考讲解和答案:
方法1:循环方法
#include <bits/stdc++.h> using namespace std; long long a,b,n=1; int main(){ cin>>a>>b; if(a==1){// 如果a等于1,任何次幂的结果都是1,直接输出1并结束程序;如果没有该特判语句,则会出现超时情况 cout<<1<<endl; return 0; } for(int i=1;i<=b;++i) if(n*a<=1e9)n*=a; else{ cout<<-1<<endl; return 0; } cout<<n<<endl; return 0; }超时的原因:
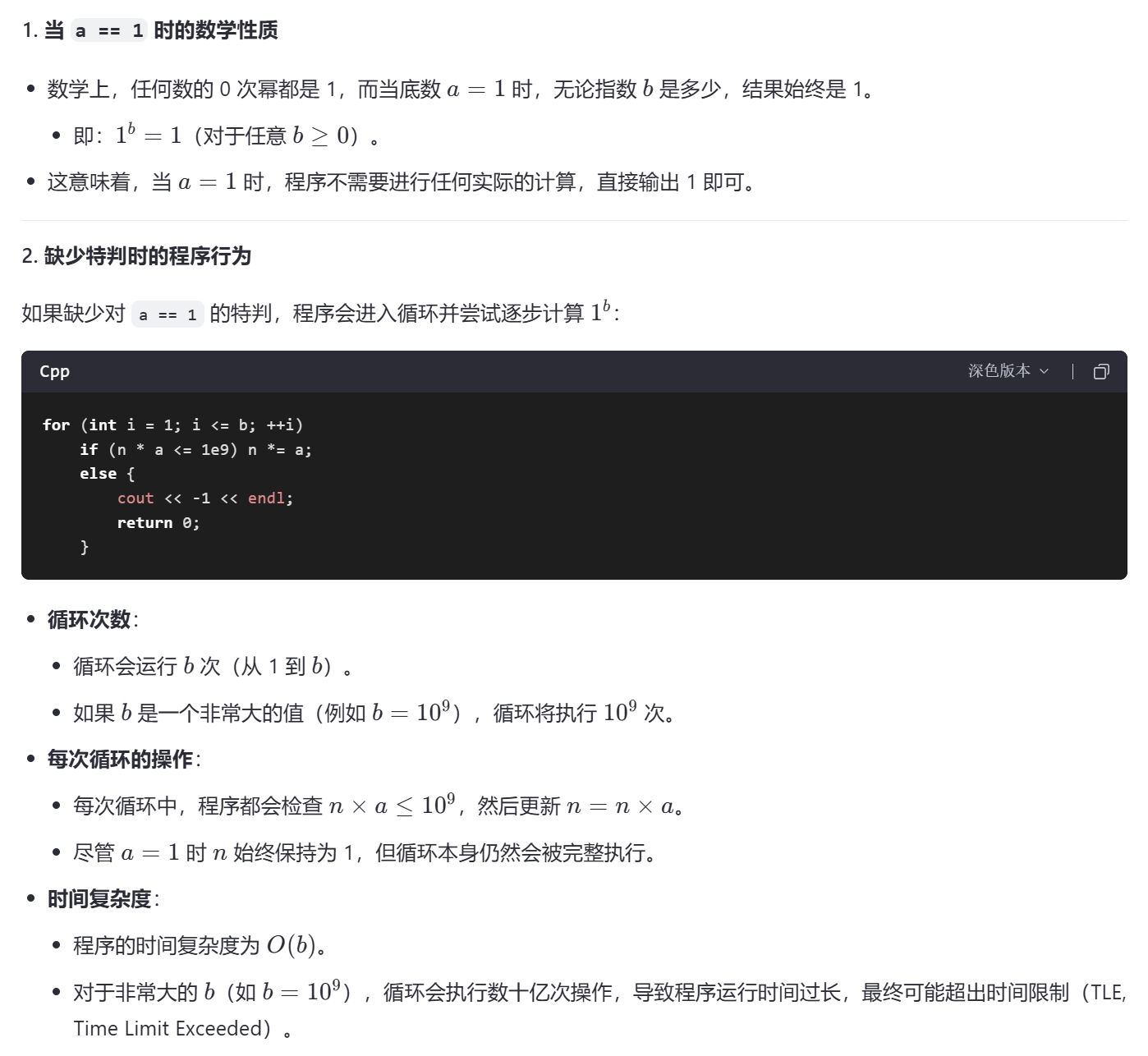
方法2:函数法
#include<bits/stdc++.h> using namespace std; int main(){ long int a; int b; cin>>a>>b; long long c=pow(a,b); if(c<0||c>1000000000){ cout<<-1; return 0; } cout<<c; return 0; }👎 4❤️ 1 -
@ 2025-4-14 12:46:22
T1 知识点和训练
第 3 题:参考讲解和答案:
方法1:数学方法
#include <bits/stdc++.h> using namespace std; int main() { int n, L, R; // 定义变量:n(除数)、L(范围左边界)、R(范围右边界) cin >> n >> L >> R; // 从用户输入读取n、L、R的值 // 计算小于等于R的n的最大倍数,再减1得到最大可能的余数 int max_remainder = (R / n) * n - 1; // 判断max_remainder是否大于等于L(即是否在[L, R]范围内) if (max_remainder >= L) { cout << n - 1 << endl; // 如果满足条件,最大余数为n-1 } else { cout << R % n << endl; // 否则,最大余数为R除以n的余数 } return 0; }方法2:暴力法(存在超时)
#include <bits/stdc++.h> using namespace std; int main() { int n,l,r; cin >> n >> l >> r; int ans=0; for (int i=l;i<=r;i++){ ans=max(ans,i%n); } cout<<ans; return 0; }👎 3🤡 3👍 2👀 2 -
@ 2025-4-7 13:12:05
T1 知识点和训练
第 2 题:参考讲解和答案:
方法1:字符数组
#include<bits/stdc++.h> using namespace std; int cnt; int main(){ string s; cin>>s; for(int i=0;i<s.size();i++) if(s[i]=='1') cnt++; cout<<cnt; return 0; }方法2:位运算
#include<cstdio> using namespace std; int ans; int main() { for (int i = 0; i < 8; i++) { if (!(getchar() ^ '1'))ans++; } printf("%d", ans); return 0; }👎 3🌿 2 -
 @ 2025-4-2 13:18:10
@ 2025-4-2 13:18:10#include<bits/stdc++.h> using namespace std; int main(){ ios::sync_with_stdio(false),cin.tie(0); int n; cin>>n; if(n & 1){ cout<<"-1"; }else{ for(int i = 23; i >= 1; i--){ if(n >> i & 1) cout<<(1 << i)<<" "; } } return 0; }❤️ 7👍 7👀 7😄 6🌿 6👎 5🤡 5🕊️ 5🤔 5😕 5🍋 4🤣 4 -
@ 2025-4-2 13:11:52
T1 知识点和训练
第 1 题:参考讲解和答案:
方法1:迭代法
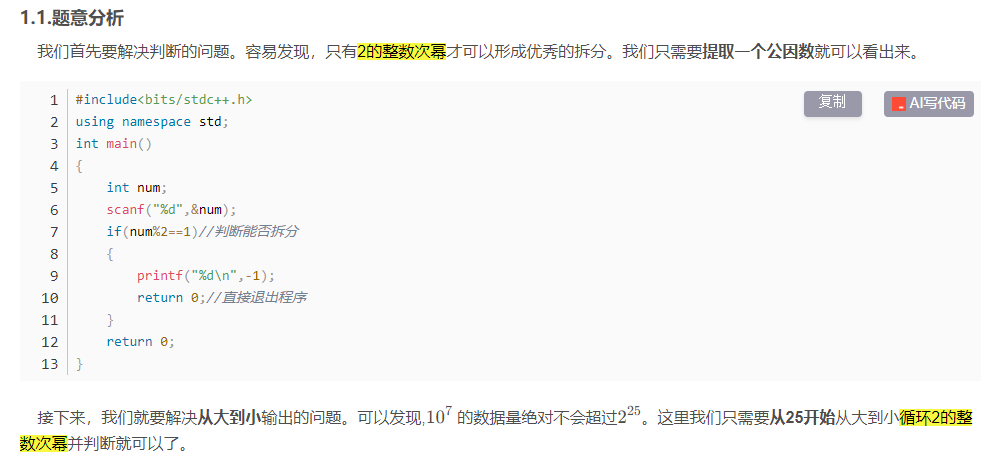
#include<bits/stdc++.h> using namespace std; int main() { int num; scanf("%d",&num); if(num%2==1)//判断能否拆分 { printf("%d\n",-1); return 0;//直接退出程序 } for(int i=25;i>=1;i--)//从大到小判断,最大不可能超过2^25 if((1<<i)<=num)//输出,1<<i代表1*2^i { printf("%d ",1<<i);//输出这个数 num-=(1<<i);//减去它 } puts("");//输出换行 return 0; }方法2:位运算

#include<bits/stdc++.h> using namespace std; int main() { int num; scanf("%d",&num); if(num%2==1)//判断能否拆分 { printf("%d\n",-1); return 0;//退出程序 } /*将一个数转化为2进制,如6=1*2^2+1*2^1+0*2^0=110(2),也就是从最高位开始判断, 第i为如果有1,那么这个数就有一个2^i*/ for(int i=25;i>=1;i--)// if((num>>i)&1)//看num左移i位后的最高位,也就是第i位是否有1,可以自己画图理解 printf("%d ",1<<i);//输出这个数 puts("");//输出换行 return 0; }方法3:递归

#include<bits/stdc++.h> using namespace std; void split(int n)//分解函数 { if(n==0)return;//递归边界 int i=1;//从1开始 while(n/2>=i)//从大判断 i<<=1;//等同于i*=2 printf("%d ",i); split(n-i);//递归处理剩下的 } int main() { int num; scanf("%d",&num); if(num%2==1)//判断能否拆分 { printf("%d\n",-1); return 0; } split(num);//调用分解函数 puts("");//输出换行 return 0; }班级同学示例:
#include<bits/stdc++.h> // 包含所有C++标准库 using namespace std; // 使用标准命名空间,避免写std:: int main(){ int a; // 声明整数变量a用于存储输入 cin>>a; // 从用户输入读取数字存入a // 检查输入的数字是否为奇数 if(a%2!=0){ cout<<-1; // 如果是奇数,输出-1 return 0; // 结束程序 } // 当剩余值大于0时继续循环 while(a>0){ int b=2; // 初始化b为最小的2的幂(2^1) // 寻找不大于当前剩余值的最大2的幂 while(a>=2*b){ // 注意:这里原代码有错误,应为2*b b*=2; // b不断乘2直到超过剩余值 } cout<<b<<" "; // 输出找到的2的幂 a-=b; // 从剩余值中减去这个2的幂 } return 0; // 程序成功结束 }👎 4👍 2🤡 2🕊️ 2
- 1

